티스토리 뷰
#include <string>
#include <vector>
#include <math.h>
using namespace std;
long long solution(int r1, int r2) {
long long answer = 0;
for(int i=1; i<=r2; i++) //x축 고정
{
long long minY = (i < r1) ? ceil(sqrt((long long)r1*r1 - (long long)i*i)) : 0; //최소 Y값
long long maxY = floor(sqrt((long long)r2*r2-(long long)i*i)); //최대 Y값
answer += (maxY-minY+1);
}
return answer*4; //4분면
}
원의 방정식을 응용한 문제다.
먼저 원의 방정식은 다음과 같다.
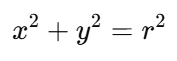
이를 응용하여 내부 원의 반지름 r1과 외부 원의 반지름 r2를 참고하면 다음과 같은 식이 성립한다.

위 식을 토대로 계산하면 또 다음과 같음을 알 수 있다.

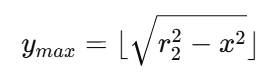
따라서 x축을 고정시켜놓고, 위 공식을 통해 최소 Y값, 최대 Y값을 구해주면 된다.
그리고 가능한 정수 값을 찾는 것이기에 최소의 경우 올림처리를, 최대의 경우 내림처리를 해서 맞춰주어야한다.
추가로 주의할 점은 x < r1인 경우이다.
이 경우에 이후 계산식이 무조건 음수로 sqrt 계산이 불가능하다.
어차피 계산식 자체가 무조건 음수이기에 y의 값은 0이상이면 모두 충족가능하다.
따라서 이 경우 y의 값은 0으로 설장한다.
이렇게 구한 최소 Y값과 최대 Y값을 통해 가능한 Y값을 누적하여 answer에 더해주고,
해당 값은 4분면의 한 케이스 이기 때문에, answer를 4배 곱하여 반환해주면 된다.
'프로그래머스 > 2레벨' 카테고리의 다른 글
| [프로그래머스 2레벨] 요격 시스템 (C++) (0) | 2025.05.19 |
|---|---|
| [프로그래머스 2레벨] 혼자서 하는 틱택토 (C++) (0) | 2025.05.18 |
| [프로그래머스 2레벨] N-Queen (C++) (0) | 2025.05.16 |
| [프로그래머스 2레벨] 지게차와 크레인 (C++) (0) | 2025.05.15 |
| [프로그래머스 2레벨] 과제 진행하기 (C++) (0) | 2025.05.07 |
